この章では、シングルモードの電磁場の量子状態のうち、代表的なものを紹介する。電磁場は、量子力学的な調和振動子の集まりとして表現できるので、調和振動子にどのような状態があるかについて考えればよい。
10pt A.光子数状態
調和振動子は、 
という交換関係を満たす生成・消滅演算子で記述できる。調和振動子で最も基本的な状態は、 
で定義される数演算子の固有状態である数状態 
である。この状態は、あるシングルモードに厳密にn個の光子が存在する光子数状態に対応する。しかし、現在の技術で実際に光子数状態を生成することは非常に困難である
。光子数状態は、位相が完全にランダムになっているが、光子数の揺らぎは全く無い。
10pt B.コヒーレント状態
古典的な電磁波は、振幅と位相が共に定まっている。このような古典的な光に対応する量子状態がコヒーレント状態である。通常のレーザーから発生する光はコヒーレント状態にあり、光学過程を記述する上で自然な基底としては、光子数状態でなくコヒーレント状態が適している。
シングルモードのコヒーレント状態 
は、ユニタリーな演算子 
を使って次式のように定義できる。
は、真空状態を表す。コヒーレント状態は、消滅演算子の固有状態であり、
また、その光子数分布はポアソン分布に従う。
の分散は、 
となる。この大きさの 
のことを標準量子限界（Standard Quantum Limit, 略して SQL）と呼ぶ。コヒーレント状態にある光を使って光通信をするとき、ビット誤り率 
を達成するのに最低限必要な光子数は、 
より、 
となる。光子数分布がポアソン分布より狭いサブポアソン的な状態にある光を使えば、最小光子数を小さくすることができる。
10pt スクイーズド状態
スクイーズ(squeeze)とは、圧縮・圧搾するという意味であるが、どのようなゆらぎを小さくするかによって、スクイーズド状態にはいくつかの種類がある。 ある1つのモードの電場は、次式のように表すことができる。
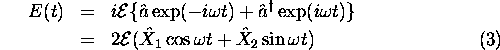
ここで、 
は、二つの直交する位相の振幅を表す演算子である。 は、 
という交換関係を満たし、 
という不確定性関係が成立する。真空状態やコヒーレント状態にある光に対しては、 
が成り立っている。直交位相振幅スクイーズド状態(quadratute-phase squeezed state)は、 のどちらかのゆらぎを、真空の持つゆらぎ 
よりも小さくした状態である。もうひとつの代表的なスクイーズド状態が、位相のゆらぎを犠牲にしながら光子数のゆらぎを縮小した光子数スクイーズド状態(photon-number squeezed state)である。コヒーレント状態、直交位相振幅スクイーズド状態、光子数スクイーズド状態のゆらぎの様子を、図1に示す。
Figure: いろいろな状態のゆらぎ。a:コヒーレント状態、b:光子数スクイーズド状態、c,d:直交位相振幅スクイーズド状態。
以下では、これら二つのスクイーズド状態について紹介する。
10pt C. 直交位相振幅スクイーズド状態
直交位相振幅スクイーズド状態を生成するユニタリー演算子 
を次にように定義する。
は、次のような性質を持つ。
シングルモードのスクイーズド状態 
は、次式のように定義できる[12]。
スクイーズド状態に対する直交位相振幅と光子数の期待値を計算すると
となる。(9)式のように、スクイーズド状態は振幅の期待値 
がゼロの場合（真空のスクイーズド状態）でも、光子数の期待値はゼロではなく、それは、実験的には、パラメトリック蛍光として観測される。
の時、直交位相振幅の分散は次のようになる。
このように、 
の不確定さは、真空の値より小さな値をとる。またこの時、スクイーズド状態は最小不確定状態になる。スクイーズド状態は、ある成分において真空のゆらぎよりも小さなゆらぎを持つが、その代償として、それと共役な成分のゆらぎは増加する。
10pt D. 光子数スクイーズド状態
次式で定義されるsine演算子とcosine演算子を考える[13]。
数演算子とsine演算子は次のような交換関係と不確定性関係を持つ。
上式は、 
の時、 
となり、光子数と位相 
の不確定性関係を表していることがわかる。
光子数[-位相]スクイーズド状態は、(15)式の不確定性関係の等号を満たす最小不確定状態として定義されており[4]、次の演算子の固有状態である[14]。
光子数スクイーズド状態の と 
の分散は、 
の時次のようになり、光子数雑音がコヒーレント状態のそれより小さくなる。
但し、このように定義される状態はコヒーレント状態を含んでおらず、実験との対応が不明確であると指摘されており、そのため、近似的に最小不確定性を満たしコヒーレント状態とユニタリー変換で結ばれた別の光子数スクイーズド状態も提案されている[15]。
